Principles of Waves

Sound is the reception of air pressure variations as electro-chemical impulses that your brain perceives as sound. The first part of this definition is what most people are familiar with, but perception is the most important factor. Music and human speech are both adapted to how the brain processes sound, so it is important to understand how the process works.

The Wave Equation

It will be helpful to cover some essential wave theory before covering the neurophysiology of sound.

\[y(t) = A \cdot \sin(f \cdot (t + \phi))\]

This is a simple wave equation \(y(t)\). Wave equations can be used to represent changes in the air, transverse wave on a guitar string, or the movement of a speaker cone. The argument \(t\) represents change over time, which for brevity can be measured in seconds.

The properties of a wave are its amplitude, frequency, and phase, which can be found in the wave equation as \(A\), \(f\), and \(\phi\) (phi) respectively. Below is a plot of the wave function with nominal values for its amplitude, frequency, and phase:

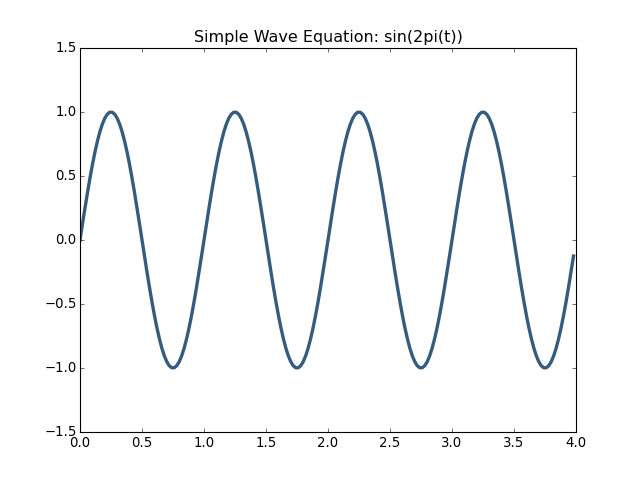
Amplitude

The amplitude of a wave is the distance it travels from its peak height to the point of equilibrium, which is zero in this plot. An increase in amplitude is perceived as an increase in volume (or intensity), and likewise a decrease in amplitude is perceived as an decrease in volume. Amplitude is often measured in the logarithmic unit of decibels (dB).

Frequency

The frequency of a wave is its rate of change, which can be measured as the distance between peaks, troughs, or other recognizable repetitions. This distance is often referred to as the wavelength, and is denoted with the symbol \(\lambda\) (lambda). The wavelength, peaks, and troughs of a cosine wave are identified in the figure below:

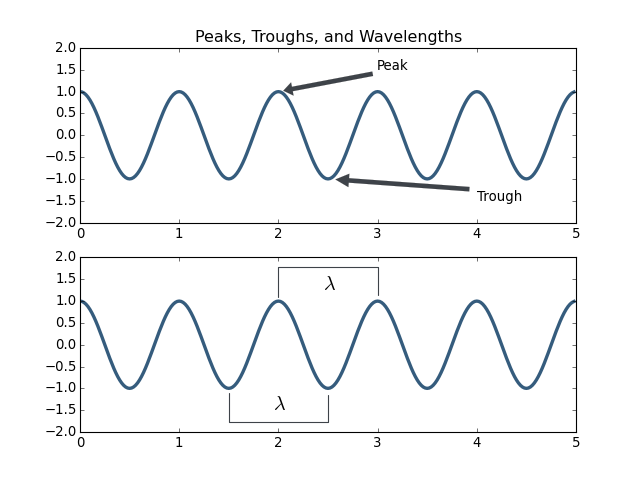
As the frequency of a wave increases the wavelength decreases, and as the frequency decreases its wavelength increases. The general shape of the wave from the start and end point of the wavelength is often referred to as the waveform.

Typically, the frequency of a sound wave is perceived as the pitch of the sound. Frequency measured in hertz (Hz), which represents the number of repetitions per second. For example, a 440Hz sound wave will repeat 440 times every second.

Phase

The phase of a wave is the initial horizontal offset for the waveform. For example, a sine wave and a cosine wave both have the same waveform, but a sine wave starts from zero and a cosine wave starts at one. In this example, a cosine wave has a phase difference of \(\frac{\pi}{2}\) (\(90^{\circ}\)) from a sine wave.

Phase itself does not affect the perception of a sound wave. One instance of phase affecting perception is when two out-of-phase waves are played together and can reinforce peaks and troughs or cancel each other out, as seen below:

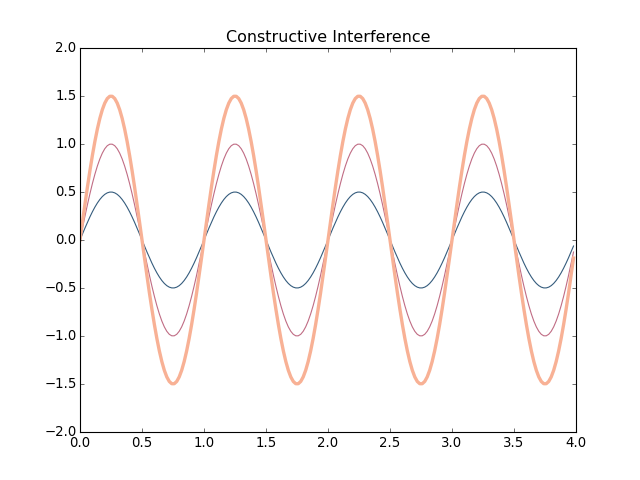
The bold outside line is the summation of the red and blue sine waves, which are out of phase from each other by \(2\pi\) causing the overall wave to increase in amplitude. This behavior is also commonly called interference, in particular this is constructive interference.

Waves that have a phase offset that is close to an odd multiple of \(2\pi\) will have destructive interference, where the peaks and the troughs are diminished, decreasing the overall amplitude. At an offset of \(\pi\) the sine waves will completely cancel out, resulting in silence.

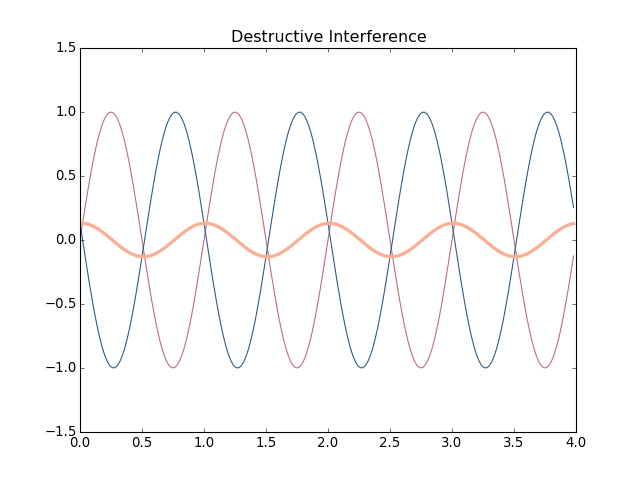
This might make more sense if you try playing with this concept, using the demo below: